Say It Again Sam Recursive Writing

Practice you struggle with recursion? If so, you're not solitary.

Recursion is friggin hard!

But that doesn't mean you can't acquire how to primary recursive interview questions. And in this post, I'll bear witness you exactly how to do that.

Whether you're brand new to recursion or you've been effectually the cake a couple times, keep reading and yous'll have your recursive interviewing to the next level.

In this post, I'm going to share with you how to sympathize any recursive code, the 6 recursive patterns you Demand to know, 10 of the most common recursive interview questions, and much more…

This is a long post, so feel free to jump around as y'all run across fit. Here's what we'll be covering:

1. What is recursion and when should you use it?
2. This is difficult. Why practice nosotros demand to acquire recursion anyway?
3. Understanding any recursive lawmaking, step by pace
4. Tail recursion, backtracking, and other core recursive concepts
5. The vi core recursive patterns to solve Whatever recursive interview question <— Advanced readers start here
6. Java vs. Python vs. C/C++. Recursion in every linguistic communication
7. The 10 about common recursive interview questions

Want to take your recursion to the next level? Check out our masterclass, Coding Interview Mastery: Recursion!

What is recursion and when should you utilize it?

Are you totally new to recursion? No idea what nosotros're talking about? Someone sent you this article and you're already lost?

Never fearfulness!

Recursion is merely a function that calls itself. In fact, you lot've almost certainly done recursion earlier even if you didn't know it.

Ever compute a Fibonacci sequence? Well that was recursion.

Nosotros all know the formula to compute the nth Fibonacci number, correct? fibonacci(n) = fibonacci(north-1) + fibonacci(n-2), fibonacci(0) = 0 and fibonacci(1) = one.

In this case, fibonacci() is our recursive part. We have 2 base cases , fibonacci(0) = 0 and fibonacci(ane) = 1.

So what does this look like equally a piece of code?

int fibonacci ( int northward ) { // Base example if ( n == 0 | | n == 1 ) return n ; // Recursive footstep return fibonacci ( n-1 ) + fibonacci ( n-2 ) ; }

Non besides bad, right?

Looking at this code, we can run into in that location are two core pieces.

First, there's the base case. The base case for a recursive function is the where our code terminates. Information technology'south the piece that says "nosotros're washed here". When n == 0 or n == 1, we know what the value should be and we can end computing anything else.

Second, nosotros have our recursive step . The recursive stride is where our function actually calls itself. In this example, y'all can see that we are decrementing n each fourth dimension.

If you're totally brand new to recursion, information technology'south worth it to dig a footling flake deeper. Khan Academy has some peachy resources on recursion that you tin can check out here .

When should y'all utilize recursion?

Recursive code is pretty absurd in the sense that you can use recursion to do annihilation that you lot tin do with non-recursive code. Functional programming is pretty much built around that concept.

Just just considering you can do something doesn't mean you should do something.

At that place are a lot of cases where writing a function recursively will be a lot more effort and may run less efficiently than the comparable iterative code. Obviously in those cases we should stick with the iterative version.

So how exercise yous know when to use recursion? Unfortunately, there's no 1-size-fits-all answer to this question. Just that doesn't mean we can't outset to narrow things down.

Here are a couple questions you can ask yourself to decide whether you lot should solve a given problem recursively:

• Does the problem fit into one of our recursive patterns?
  In the recursive patterns section, we volition see 6 different common recursive patterns. 1 of the easiest ways to decide whether or non to utilize recursion is simply to consider if the problem fits into one of those patterns.
• Does the problem patently break down into subproblems?
  Many people define recursion as "solving a problem past breaking information technology into subproblems". This is a perfectly valid definition, although the 6 recursive patterns become more than precise. However, if y'all see a style to intermission a problem downward into subproblems, then information technology can probable be solved easily using recursion.
• Could the trouble be solved with an arbitrary number of nested for loops?
  Have you ever tried to solve a problem where it would be easy to solve if you could have a number of nested for loops depending on the size of the input? For example, finding all North-digit numbers. We can't do this with actual for loops, but nosotros can do this with recursion. This is a expert indicator that you might want to solve a trouble recursively.
• Can you lot reframe the problem as a search trouble?
  Depth-first search, ane of the patterns we will see, is incredibly flexible. It can be used to solve near any recursive problem by reframing it as a search problem. If yous meet a problem that can be solved by searching, then y'all have a proficient recursive candidate.
• Is information technology easier to solve information technology recursively than iteratively?
  At the end of the day, this is what it comes down to. Is it easier to solve the problem recursively than information technology is to solve it iteratively? Nosotros know that any problem can be solved either recursively or iteratively, so you just accept to decide which is easier.

Don't do some other coding interview…​​

…Until you've mastered these l questions!

This is hard. Why do we need to learn recursion anyway?

So often I get emails from students telling me how much they struggle with recursion. In fact, when I search in my inbox for "recursion", this is what I see:

That's a lot of friggin emails.

So what if we just skip learning recursion? What if we just stick with Fibonacci and some other simple recursive problems. Is it really that much of an issue?

Aye!

Recursion comes upward EVERYWHERE. In fact, I pulled upwardly a few of the most common Google interview questions on Leetcode and expect what I found:

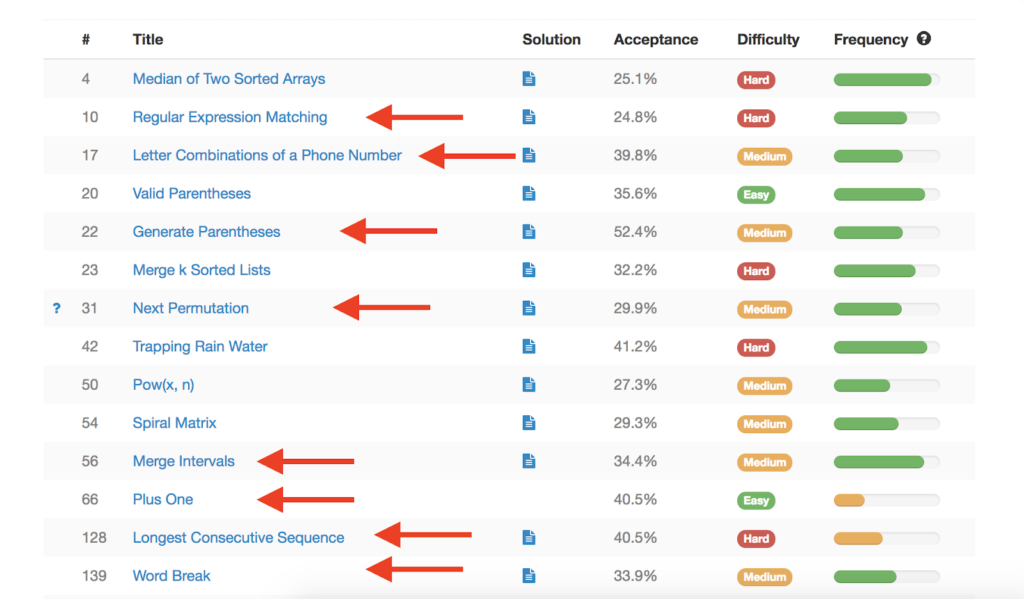
Out of these 14 questions, more than 50% of them either require or directly chronicle to recursion.

Ok, I'm gonna repeat that considering it'due south really important:

FIFTY Percent (half!!) of Google'southward interview questions Crave Recursion .

Fifty percent of Google'south interview questions require recursion. Click To Tweet

Not to mention… those other questions? They could be easily solved with recursion if you knew your stuff.

Is at that place ANY other data structure or algorithm that tin say that?

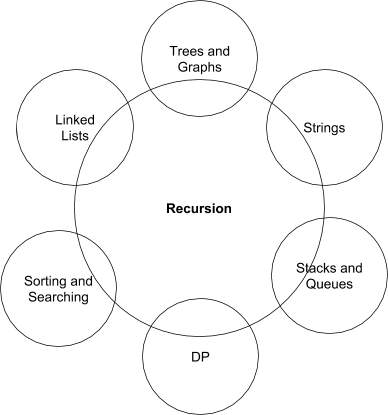
Recursion is so fundamental because it overlaps with literally every other category of trouble that nosotros could get asked:

• Linked lists? Print a linked list in opposite order.
• Strings? Decide if a string is a palindrome.
• Trees and graphs? Have fun doing an iterative DFS.
• Dynamic programming? Okay exercise you get my betoken? This is all recursive.

If nosotros were to draw out our categories equally a Venn diagram, information technology would expect something like this:

⇡ How this interview will kick your butt if you don't know Recursion ⇡

If we don't take the time to really larn recursion, we're just screwing ourselves. Patently and simple.

And while recursion may seem overwhelming, in the rest of this post I'm going to break down for you exactly how to approach information technology to make information technology less intimidating and set y'all up for interview success.

Which leads us to the first primal footstep…

How to understand whatsoever recursive lawmaking, step by pace

Earlier we even get into writing our ain recursive code, it's disquisitional that we have a clear agreement of how recursive code actually works. Later on all, how can you write something that you don't understand.

The problem here is that recursive code isn't exactly straightforward.

Well-nigh code executes in a linear fashion. We beginning at the top of the file and keep running until we get to the bottom. If in that location'due south a loop, we loop through until we ultimately get out the loop, but and then we proceed going. Without recursion (and go-to statements, and then help me God), that is as complicated as our not-recursive code will get.

Just as shortly every bit we throw in recursion, all bets are off.

As before long as we make a recursive call, we are jumping out of the original function and computing something completely different before we always even come back to the original function.

Permit's look at a simple example of how the order of execution for recursive functions changes.

Consider the post-obit lawmaking:

void f ( int n ) { if ( n == 0 ) return ; f ( n-1 ) ; print ( northward ) ; }

What is the output of this code?

If we read the code in the order that it's written, and then nosotros might think that it would print the output of f(v) every bit 5, iv, 3, 2, 1. Afterall, the outer office prints 5 beginning, and and then information technology afterwards gets decremented.

Unfortunately, though, this would be wrong. We have to evaluate the recursive call first before we can proceed to the finish of the role.

Therefore, our lawmaking executes every bit follows:

f ( 5 ) f ( 4 ) f ( 3 ) f ( two ) f ( 1 ) f ( 0 ) impress ( one ) print ( 2 ) print ( 3 ) impress ( 4 ) print ( 5 )

Equally you tin see, the proper output of this office is ane,two,three,4,5.

The key thing to empathise here is that our output is not ever going to occur in the lodge that it appears in our code.

So how do we accurately compute the output?

The fundamental to understanding any recursive lawmaking is to walk through the code step-by-step. Y'all are at present the compiler.

The most important thing to exercise is to walk through the code exactly as the compiler would. As soon every bit you start assuming how the lawmaking will behave and not reading through it line-by-line, y'all're screwed.

In this video, I show you exactly how to do this:

Here are the most important tips to doing this effectively:

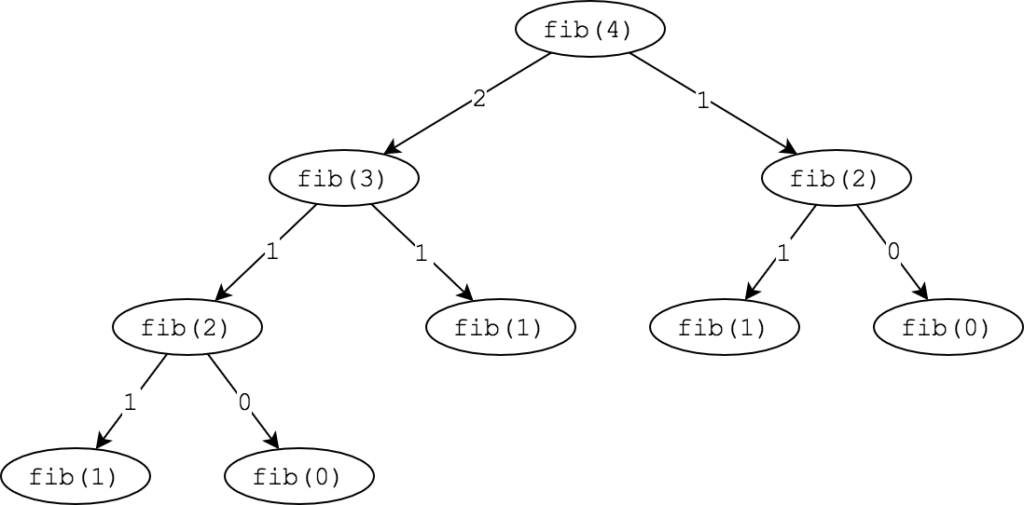
• Draw the recursive tree. Recursive functions tin act like a tree. The parent is the main role call and each recursive call made is a child node. The tree structure can exist actually useful considering information technology helps you lot to easily keep track of variables. Hither is what a tree might look like for the Fibonacci function.
• Practice non lose rail of your variables. This is absolutely disquisitional. As functions get more complicated it becomes harder and harder to actually store everything in your head, particularly since you have to do your recursion out of order. The tree will assistance you lot with this.
• Practice. I know this may not sound like the most fun task, but agreement recursive code is critically of import. If you can understand the recursive lawmaking that other people write and why it works it will make information technology exponentially easier for you to write your own recursive lawmaking.

Start with some elementary bug. Try to do this for a Fibonacci or factorial problem and then work your way up. Yous tin can find tons of examples of recursive code that others have written. Grab a random piece of code and try to interpret what it's doing.

Then compare your results to what y'all get when you actually run the code. Yous'll gain so many insights on how recursive lawmaking works through this procedure.

Tail recursion, backtracking, and other core recursive concepts

Okay now we know what recursion is, we know why nosotros need information technology, and we know how to sympathise a piece of recursive code when we see it.

Information technology'due south about time that we offset getting into the meat of how to write our own recursive code.

In this section we're going to start with some of the virtually important and asked about (although non necessarily both, ahem tail recursion) topics related to recursion.

Render types

To start with, it is critical that we go over strategies for returning values from our recursive function. While some recursive functions may but print the results, in many cases, we are going to want to return a specific issue to the caller. There are multiple different ways that we can do this recursively, some of which are ameliorate than others.

Global Variable

The first option (and the only one hither that I'd say you should probably never use) is to shop your outcome into a global variable. We all know that global variables aren't a nifty solution when in that location is some other option, and then attempt to avoid this if possible.

For demonstration purposes, let's look at a function that counts the number of even values in an array. Hither'southward how we could write this code using a global variable:

int globalResult ; void countEvenGlobal ( int [ ] arr ) { globalResult = 0 ; countEvenGlobal ( arr , 0 ) ; } void countEvenGlobal ( int [ ] arr , int i ) { if ( i >= arr . length ) render ; if ( arr [ i ] % 2 == 0 ) globalResult++; countEvenGlobal ( arr , i+1 ) ; }

The key here is that we volition simply create a global variable and update the value as we recurse through our lawmaking. Whenever we find an even value in our assortment, we merely increment the global variable, similar to how nosotros might solve this problem iteratively.

Passed Variable

A better option that is similar to using a global variable is to apply a passed variable. In this case we are going to pass a variable to our recursive function that nosotros volition update with the result as we become. Essentially this is like having a global variable except that information technology is scoped to our role.

Our code looks like this:

class ResultWrapper { int outcome ; } int countEvenPassed ( int [ ] arr ) { ResultWrapper result = new ResultWrapper ( ) ; result . result = 0 ; countEvenPassed ( arr , 0 , event ) ; return effect . result ; } void countEvenPassed ( int [ ] arr , int i , ResultWrapper result ) { if ( i >= arr . length ) return ; if ( arr [ i ] % 2 == 0 ) result . upshot++; countEvenPassed ( arr , i+1 , consequence ) ; }

Note in this code, if we are using a language like Coffee, nosotros accept to use some sort of ResultWrapper form because nosotros cannot directly pass a arrow to our function and nosotros will exist updating the value equally we go.

The advantage of this arroyo is that information technology is generally the easiest for virtually people to understand. Information technology as well gives us the opportunity to exercise tail recursion, if that is something that our language (and the problem) supports.

Build the upshot as nosotros return

Our third strategy is a bit more hard to sympathise because we are essentially doing the piece of work that we need to do in reverse order. We will return partial values as we return from our recursive calls and combine them into the outcome that nosotros want.

The reason that this strategy is critical is that information technology volition make it possible for us to employ the FAST Method to solve dynamic programming problems. If we utilize i of the previous two approaches, we are not isolating our subproblems and so it becomes incommunicable for us to actually cache the values that we want.

Hither is what our solution might look like:

int countEvenBuiltUp ( int [ ] arr ) { render countEvenBuiltUp ( arr , 0 ) ; } int countEvenBuiltUp ( int [ ] arr , int i ) { if ( i >= arr . length ) return 0 ; int result = countEvenBuiltUp ( arr , i+1 ) ; if ( arr [ i ] % 2 == 0 ) outcome++; return outcome ; }

For the most part, you tin use these return strategies interchangeably for different recursive issues.

Don't bother practicing using global variables, since you actually should never employ that in your interview. Nonetheless, I would recommend practicing both of the others. Try doing a practice problem both means. Run into what the similarities and differences are. The extra practice volition do yous proficient!

Backtracking

What is backtracking?

Backtracking is an essential strategy that nosotros employ in recursion. It substantially allows us to effort different possible results without actually knowing ahead of time what the correct outcome is.

Consider the Knight'southward Tour problem. In this trouble, nosotros want to find a path that a knight tin can follow on a chessboard where information technology will visit each square exactly once.

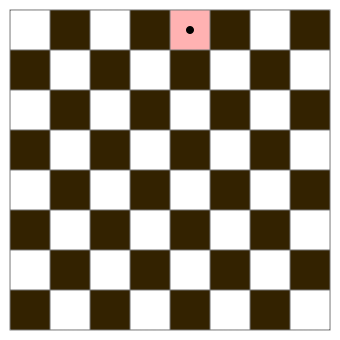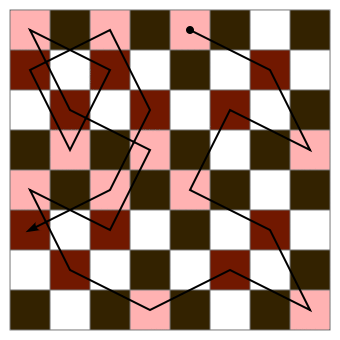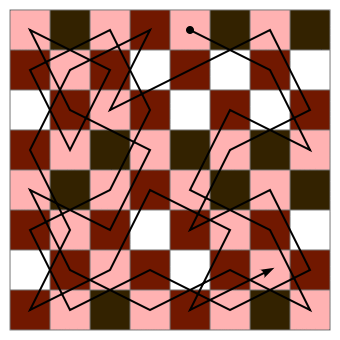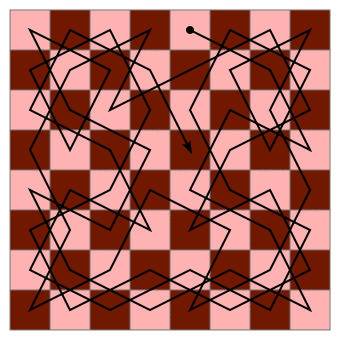
We don't actually know what the right more is to make ahead of time and a knight can make upwards to 8 unlike moves from whatever one square, then we just have to selection a motility at random.

But patently not all combinations of moves will take us through a valid path. Some moves might trap u.s. in a corner that we tin't become out of without visiting the same square twice.

So what do we do? We "backtrack".

The idea behind backtracking is simply that we retrace our steps backwards then attempt a unlike path. This allows us to endeavour every different path until we ultimately find ane that is valid.

Some other example of this that you're likely already familiar with is depth-first search in a tree. When we are looking for a node in a tree, nosotros consider the leftmost co-operative get-go. So what happens if we don't notice the node we're looking for? We backtrack.

We go back up 1 level and endeavor the other child of the parent node. If we still haven't found what we are looking for, we go back up the tree even further. This continues until we find what nosotros are looking for or accept gone through the entire tree.

Some common backtracking problems include:

• 0-1 Knapsack
• Sudoku Solving
• Northward Queens
• And many more…

A annotation on backtracking : A lot of people hear "backtracking" and they stress out about it, but my estimate is that if y'all've washed any recursion in the past, you're already familiar with the basic concept. Don't stress as well much about this ane specifically. Just make sure you understand how to implement the six recursive patterns and you'll learn how to practise backtracking as a side-result.

Tail recursion

Okay this is the nearly unnecessarily worried well-nigh concept in all of recursion. Tail recursion almost never comes up in an interview and isn't fifty-fifty supported by most major programming languages .

That said, I'm non opposed to giving it it's off-white representation here. So let's cover the basics of tail recursion.

Tail recursion is an optimization technique that you can use to better the infinite complication of a minor subset of recursive problems. To sympathise how this works, we exercise need to talk about space usage for a second.

When you make recursive calls, the estimator needs to save the state of the current function (all the variables, the electric current position that yous're executing at, etc) and then that you can return back subsequently the cease of the recursive call.

Therefore, for every recursive call you make, you are using some infinite on the call stack. The more recursive calls you lot make, the more space you're using.

Tail recursion allows us to avoid having to use extra space. Imagine that you write a function where the very final line of the part is the recursive phone call that immediately returns. Then exercise y'all really need to save the previous role country on the call stack?

No. You can just return the value from the deepest level of your recursion directly to the top.

That is what tail recursion does for us. If we accept a single recursive call that is the very terminal thing before nosotros return, so nosotros tin can optimize out the extra stack space.

To await at our simple example from earlier, which of these is tail recursive?

void f1 ( int n ) { if ( n == 0 ) return ; f1 ( n-1 ) ; print ( n ) ; }

Or

void f2 ( int n ) { if ( n == 0 ) return ; print ( n ) ; f2 ( due north-1 ) ; }

Based on our definition, you can see that in f2(), the very last thing we do is our recursive telephone call. f1() prints later we make the recursive call so nosotros can't optimize it considering nosotros are going to need to return back to the previous part then that we tin call print(north).

So in limited circumstances, tail recursion can be useful. Information technology is particularly useful while doing functional programming, since you are frequently doing basic things like iteration recursively that can be easily optimized.

However, well-nigh of the time, tail recursion won't exist helpful to us. Chances are the language that you're using won't back up it and on elevation of that, many of the examples that we will meet in our interviews will require us to make multiple recursive calls within our office. If you have multiple calls, they tin't both be the last thing before we render and so tail recursion is out of the question.

Recursive Time and Space complexity

Fourth dimension and space complexity for recursive problems tends to pose quite a challenge. Considering recursive issues are so hard to parse in the start place, it is oft non-obvious how we would compute the complication.

However on the bright side, there are a couple of heuristics that nosotros tin use to aid us.

Time Complication

Retrieve when we represented our recursion equally a tree structure? Well that tree structure tin show us very conspicuously the number of recursive calls nosotros're making.

And simply put, the time complexity is going to be O(number of recursive calls * work per recursive phone call).

With this formula, nosotros are now able to simplify dramatically into two components that we can more easily calculate.

Beginning, let'southward talk about the number of recursive calls.

How do nosotros guess the total number of recursive calls without drawing out the whole tree? Well if we wanted to compute the number of nodes in a tree, nosotros can await at the height of the tree and the branching factor .

The height of the tree is simply how deep our recursion goes. For example if you lot keep recursively calling f(northward-1) and your base case is when n == 0, then our depth is going to be O(n), since we keep decrementing until n reaches 0. If nosotros have multiple different recursive calls, nosotros only consider whatever the maximum depth is (recollect that Big Oh is an upper jump).

The branching cistron is also fairly straightforward to figure out. The branching factor is defined as the maximum number of child nodes any parent has in a tree. For instance, if we have a binary tree, the branching cistron volition be 2.

To find the branching factor of our recursive tree, we simply need to look at the maximum number of recursive calls. In our Fibonacci office, we telephone call fibonacci(due north-1) and fibonacci(due north-two) every time, which gives us a branching factor of 2.

If we said:

int f ( n ) { if ( n == 0 ) return 0 ; int sum = 0 ; for ( int i = 0 ; i < n ; i++) { sum += f ( northward-i ) ; } return sum ; }

What would be the branching cistron hither?

At first glance, it seems like information technology will exist difficult to compute. Afterward all, the branching factor depends on n and n keeps changing.

But call back nosotros only demand the worst instance hither. Then we don't need to consider every example merely what is the worst case branching factor, which in this case is n.

Finally, now that nosotros have the branching factor and the height of our recursive tree, how tin we apply these to find the time complexity of our recursive function.

We tin can utilize the following heuristic:

Number of nodes = O( branching_factor depth_of_recursion )

Knowing the number of nodes, nosotros get that our total time complexity is:

O(branching_factor depth_of_recursion * work_per_recursive_call)

Work per recursive call is simply the corporeality of work that we're doing in our function other than when nosotros call it recursively. If we accept whatsoever sort of for loop, such every bit in the example to a higher place, our work per recursive call will be proportional to that loop, or O(due north) in this case.

That gives us a time complexity of O(n due north * n) for the function above.

Infinite complexity

Recursive infinite complexity is a bit easier for us to compute, but is also not exactly trivial.

The space does not depend on the branching gene, only on the height and then amount of infinite used per recursive call.

When we think about this for a minute, information technology makes sense. The branching factor leads to multiple unlike paths through our recursive tree. We take to consider each of these separately for the time complication because fourth dimension is additive. At that place is no way to reuse time.

Space, however, tin be reused. Each time nosotros recurse downwardly, we volition be using more and more than space. However, once we return from our recursive function, we clear up space that can be reused for the next path.

This gives us a formula for our space complexity of simply:

O(depth_of_recursion * space_per_recursive_call)

It is, still, important to recall that recursion does actually use up infinite, since that is something that many people ofttimes tend to forget.

Don't do another coding interview…​​

…Until y'all've mastered these 50 questions!

The half-dozen core recursive patterns

I of the main reasons why people tend to find recursion so hard is that they don't have a mental model for how to view recursion as a whole.

When you await at every recursive trouble and see how different they are, information technology can be really difficult to figure out what is going on.

Not merely that, just if every problem seems completely different, how tin can you ever feel confident that you will exist able to solve a problem in your interview.

Afterward combing through dozens of common recursive issues, I've categorized all recursive issues into one of 6 categories. These 6 categories, based around the core pattern used to solve the problem, allow us to put a finite spring on the scope of recursive issues that we could need to solve.

If y'all understand each of these patterns and how to code them, then y'all can apply these concepts to well-nigh any recursive problems that might come upwardly in your interview. These vi patterns are Iteration , Subproblems , Pick , Ordering , Dissever & Conquer , and Depth Get-go Search . For the remainder of this section, we volition go into each in more particular.

Iteration

Every bit you hopefully know, whatever problem that tin exist solved recursively tin too be solved iteratively and vice versa. This is a fundamental concept backside functional languages, where you utilise recursion to do everything; there are no loops.

While this is non something that you're often going to need to practice recursively, this blueprint tin can come in useful once in awhile, particularly if yous want to be able to refer back to items you've looped through previously.

For example, consider the problem of press a linked listing in reverse lodge. In that location are plenty of approaches nosotros can take for this problem, only recursion is uniquely concise:

void printReverse ( Node n ) { if ( n == null ) return ; printReverse ( n . next ) ; impress ( n . val ) ; }

For iteration, we simply make our recursive call on the remainder of our inputs, either by passing in the side by side node (as we did in a higher place) or by incrementing some alphabetize. While this doesn't come besides often, this is one of the simplest applications of recursion.

Subproblems

Hither nosotros have what almost people probably remember of when they think of "recursion": Breaking down a problem into its subproblems. Technically, you could use this pattern to solve whatsoever recursive trouble, but the advantage of the other patterns is that they get much more specific nigh helping yous practice that.

With all that being said, there are some issues that just lend themselves to being broken downwardly into subproblems.

I example of this is the Fibonacci problem that we've talked most earlier in this post. In that case, even the mathematical definition of a Fibonacci sequence is recursive.

Another problem that oft comes up is the Towers of Hanoi problem . In this case, nosotros can simply break downwardly our problem by because the subproblem of moving the pinnacle n-ane disks. If we can motion the elevation n-1 disks, we simply move all of them to the middle pivot, motility our bottom disk to the destination pin, and then movement the above disks again over to the destination pivot. This works because all of the disks higher up our bottom pin are not affected by any pins below them.

In problems like this, yous have to expect for those subproblems with which to interruption up the trouble. Yet, in that location aren't too many bug in this category, since most can be more explicitly solved with one of the following patterns.

Selection

This is my favorite design to test people on because information technology is one of the most mutual patterns to come up in recursion (and dynamic programming). In this pattern, we are merely finding all of the combinations of our input that match a certain criteria.

Consider for example the 0-1 Knapsack Problem . In this problem, we take a series of items that have weights and values. We desire to figure out what the maximum value is that we can achieve while remaining under some stock-still weight.

Many people recognize this every bit a dynamic programming problem, since it'due south a classic case, but permit'southward look at it from a recursive standpoint.

What would be a brute force solution to this problem? Well we can hands validate for a given combination of items whether it is under the maximum weight, and nosotros can also hands compute the weight for any combination. That means if we could just generate all the dissimilar combinations, nosotros could figure out the optimal answer.

Figuring out all the combinations is the core of a selection problem. I like the term "selection" because the way our lawmaking works is to simply include/exclude, or "select", each item in our list.

The brute strength code to generate all combinations might wait something similar this (this is simplified, just you lot go the thought):

1 2 3 iv 5 vi 7 viii 9 10 11 12 13 14 15 16 17 eighteen 19 xx 21

List < Listing < Integer > > combinations ( int [ ] n ) { List < Listing < Integer > > results = new LinkedList ( ) ; combinations ( n , 0 , results , new LinkedList < Integer > ( ) ) ; render results ; } void combinations ( int [ ] n , int i , List < List < Integer > > results , List < Integer > path ) { if ( i == n . length ) { results . add together ( path ) ; return ; } Listing < Integer > pathWithCurrent = new LinkedList ( path ) ; pathWithCurrent . add together ( n [ i ] ) ; // Find all the combinations that exclude the current item combinations ( n , i+1 , results , path ) ; // Find all the combinations that include the electric current item combinations ( n , i+one , results , pathWithCurrent ) ; }

Once we sympathize this basic blueprint, we can outset to make optimizations. In many cases, we may actually be able to filter out some combinations prematurely. For instance, in the Knapsack problem, we can limit our recursion to only consider combinations of items that stay below the prescribed weight.

If you spend the bulk of your fourth dimension on whatsoever one pattern, it should be this ane. It comes up then frequently in so many different forms. Some expert issues to get your started are 0-1 Knapsack , Word Break , and North Queens .

Ordering

This pattern is the permutation to Selection's combination. Substantially here we're looking at any case in which nosotros want to consider dissimilar orderings of our values. The almost straightforward problem here is simply to figure out all of the permutations of a given set of elements, although just similar with selection, we may add together in additional restrictions.

Some examples of bug that fall under this category are Bogosort (sorting a list of items by generating all permutations and determining which is sorted), finding all numbers that tin be made from a set of digits that friction match a certain property, determine all palindromic strings that tin be fabricated from a set of characters, and more.

In its most simple class, this is ane fashion that nosotros can brute force generate all permutations of a listing. You tin also see an culling approach here:

1 2 3 4 v 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

Listing < List < Integer > > permutations ( Fix < Integer > north ) { List < List < Integer > > results = new LinkedList ( ) ; permutations ( northward , results , new LinkedList < Integer > ( ) ) ; render results ; } void permutations ( Set < Integer > north , List < List < Integer > > results , List < Integer > path ) { if ( northward . isEmpty ( ) ) { results . add ( path ) ; render ; } for ( int i : n ) { // For at present ignore concurrent modification upshot n . remove ( i ) ; Listing < Integer > pathWithCurrent = new LinkedList ( path ) ; pathWithCurrent . add ( i ) ; permutations ( north , results , pathWithCurrent ) ; n . add ( i ) ; } }

As you can hopefully see, at that place is a lot of similarity between this solution and the combinations solution above. By understanding these ii patterns and their variants, you can embrace a huge number of the dissimilar possible recursive issues you might be asked in your interview.

Divide and Conquer

If you know virtually some of the common applications of recursion, you probably saw this one coming. Separate and conquer is the courage to how nosotros use techniques such equally mergesort, binary search, depth first search, and more than. In this technique, we endeavour to pause the problem space in half, solve each half separately, and then come back together.

Near frequently, this pattern is used equally part of common algorithms that y'all should already know, such as the one I mentioned above, but there are a handful of problems for which this can be valuable.

For example, consider trying to determine all of the unique binary trees that we can generate from a set of numbers. If you choice a root node, you only need to generate all of the possible variations of a left and right subtree.

Consider trying to find the maximum and minimum value of a listing using the minimum number of comparisons. One way that nosotros can exercise this is past splitting the listing repeatedly, much the same every bit how we would practise mergesort.

This technique by and large applies to tree and sorting/searching bug where we will be splitting the problem space then recombining the results.

There is besides a slightly different case in which D&C is very useful: Trying to find all of the ways to group a set. Imagine, for example, that you accept a mathematical office. Yous want to decide all of the different means that you can grouping the arguments. This can be done by recursively trying splitting your formula at every unlike point. Here is an example of what this code might look like. It uses a string, but demonstrates the same concept:

1 2 iii 4 five 6 7 8 9 ten 11 12 13 14 15 16 17 18 nineteen 20 21 22

List < String > parentheses ( String s ) { if ( s . length ( ) == 1 ) { List < String > result = new LinkedList < String > ( ) ; result . add ( due south ) ; return issue ; } List < String > results = new LinkedList < String > ( ) ; for ( int i = 1 ; i < s . length ( ) ; i++) { List < String > left = parentheses ( s . substring ( 0 , i ) ) ; List < String > right = parentheses ( s . substring ( i , south . length ( ) ) ) ; for ( String s1 : left ) { for ( String s2 : right ) { \ results . add together ( "(" + s1 + s2 + ")" ) ; } } } return results ; }

In this case, we take the string and we endeavour finding every dissimilar midpoint. For example "abcd" becomes "(a)(bcd)" , "(ab)(cd)" , and "(abc)(d)" . Then we recursively apply this to each of the halves of the string.

Depth Beginning Search

Depth first search is our final pattern that our recursive functions can fall under. Information technology's also one that we'll likely find ourselves using a lot. That's because DFS (and BFS) are used extensively whenever we are doing anything with copse or graphs.

In terms of the details of trees and graphs, I'1000 not going to get in depth here. In that location is way too much to cover so I'grand going to exit them to their ain study guides.

The main important thing with DFS is to understand how not only to search for a node in a tree or graph but also how to really discover the path itself. If you lot tin't exercise that, you lot're severely limiting what you can actually do.

Here is what the code might look like to find the path to a specific node in a tree:

1 2 3 4 5 6 7 8 9 x 11 12 13 14 xv 16 17 18 19 20 21 22

List < Node > pathToNode ( Node root , int val ) { if ( root == goose egg ) render cipher ; if ( root . value == val ) { List < Node > toReturn = new LinkedList < Node > ( ) ; toReturn . add ( root ) ; return toReturn ; } List < Node > left = pathToNode ( root . left , val ) ; if ( left != null ) { left . add ( 0 , root ) ; return left ; } List < Node > correct = pathToNode ( root . right , val ) ; if ( correct != null ) { right . add ( 0 , root ) ; return right ; } render zip ; }

And in that location's not that much more to information technology than that. In most cases, you volition utilize depth first search as part of a larger trouble, rather than actually having to alter it in any significant way. Therefore the almost important affair is agreement the core of how DFS works.

With these vi recursive patterns, yous volition be able to solve well-nigh any recursive problem that you could see in your interview. The key is to look for those patterns in the problems that y'all are solving. If you come across the pattern, use it. If not, try something else. Unlike patterns will work meliorate for different people, so practice what feels correct to you.

Java vs. Python vs. C/C++. Recursion in every language

While the core recursion concepts do remain the same in every language, information technology is e'er important that nosotros make the advisable distinctions. In this section, we'll briefly embrace the differences and peculiarities of doing recursion in different common languages.

If you haven't decided what language yous are going to use for your coding interviews, check out this post.

Recursion in Java

Coffee remains 1 of the two nearly popular languages for coding interviews. As a language, Java is great because it is yet widely used, and while tends to be more verbose than Python, it is easily understood past nearly any interviewer.

Key characteristics of Coffee recursion that we should keep in mind:

• No pointers. This is likely the characteristic that has the most direct consequence on writing recursive code. Since there are no pointers, if we want to use a passed variable to store the return value, we need that to be an object. Even if we're just returning an integer or String, we will need to wrap those in an object that can be passed past reference.
• No tail recursion. Java does not optimize for tail recursion, so while information technology may be nice to mention tail recursion in your interview, it has no practical value when it comes to solving the trouble.
• Strings are immutable. While this doesn't necessarily relate to recursion, it is fairly common that we want to modify strings as part of our recursive function. We can do that, but it is critical to realize the hit that we take to the time complexity if we do that. Every time we modify a string, the whole string has to be copied, which takes O(northward) time.
• References are mutable. When nosotros add a listing to our outcome, if nosotros continue modifying the list, it continues changing. Therefore if we are saving our result and so modifying it to generate other results, nosotros demand to brand certain that we copy that outcome.

Recursion in Python

While I would never say that you should do all your interviews in Python only because Python is easier, if yous know information technology well, it is certainly a great linguistic communication to use for your interviews. Python tends to lead to much more curtailed code.

Fundamental characteristics of Python recursion that nosotros should keep in mind:

• No tail recursion. Again, every bit we talked about in that section, tail recursion isn't supported by many languages. There is a third-party module that can do tail optimization, but it is not build into stock Python implementations.
• Be careful about actress work. Python is great in a lot of ways, but there is ane major issue with it: It ofttimes conceals how much piece of work is being done. In the interest of ease of use, there are lots of very simple operations that you can do in Python that do not take abiding time. Be certain that y'all're aware of what yous're doing.
• Know when you're mutating and when you're not. While Python doesn't have pointers in the way that C does, information technology generally does laissez passer by reference so it is possible for y'all to mutate values. You tin can learn more near how to exercise this properly in Python here .

Recursion in C/C++

Recursion in C and C++ is more often than not pretty similar to Python and Coffee except we practise have a few advantages, equally we'll encounter.

Primal characteristics of C/C++ recursion that we should go along in mind:

• Pointers! Because nosotros have pointers, returning values becomes a lot easier. All we have to do is laissez passer the accost of the variable that we volition be updating in our result and update the value appropriately. This is one of the ways in which C is really easier than Coffee.
• Strings are mutable. This is another quirk that can make our lives much easier. Because strings are simply pointers to character arrays, nosotros can modify them however we want in C and easily create substrings without having to incur the overhead of recreating an immutable object.
• Tail recursion. This depends on the specific compiler, only in most cases if you use ane of the optimization flags, you tin optimize out the tail recursive calls in C.

Practise problems

At present that you know all of the essentials for solving recursive problems in your interview, the most of import thing is to practice. By practicing unlike problems and applying the 6 recursive patterns, you will be well on your manner to mastering recursion.

In this section, I've shared several practice problems for each of the 6 recursive patterns. Simply if you lot don't practice properly, they won't exist of utilise to you. I recommend you practice using the following steps:

1. Attempt the problem on your own.
2. If you become stuck, wait at the solution and try to understand why you got stuck.
3. Go back and try to solve the problem completely on your own. DO NOT look at the solution.
4. If y'all get stuck, get dorsum to Step 2.
5. Repeat until you tin can solve the problem on your ain.

With this approach, you ensure that you are really understanding the problem and non just convincing yourself that y'all know it.

And without further ado, practice issues…

Iteration

• Insert an item at the bottom of a stack
• Print a linked listing in contrary lodge
• Detect all substrings of a string

Subproblems

• Towers of Hanoi
• Is a string a palindrome?
• Stair steps

Choice

• Find all combinations of a fix of inputs
• 0-1 Knapsack
• Find all means to interleave 2 strings

Ordering

• Detect all permutations of a set of inputs
• Observe all permutations when the input includes duplicates
• Find all Northward-digit numbers whose digits sum upwards to a target

Divide and Conquer

• Implement binary search
• Implement mergesort
• Discover all unique binary search trees

Depth-first Search

• Find all paths betwixt two nodes in a graph
• Knight probability
• Greatest product path

See all of our recursive interview questions here.

Pulling it all together

Phew…

That was a lot of stuff, wasn't information technology. Merely you stuck with it until the end!

The fundamental now is to become started. Whether y'all only option one of the recursive patterns, attempt walking through some sample recursive code, or simply jump straight into a practice problem, all the knowledge in the world isn't going to help you unless you know how to execute.

Start practicing, work through this material sequentially and spend a little bit of time every day. With practice, you can become a recursion primary.

Desire to become deeper with x+ hours of video instruction? Check out our premium recursion course, Coding Interview Mastery: Recursion.

samuelhencerel.blogspot.com

Source: https://www.byte-by-byte.com/recursion/

Share this post