what is used to find the relative age of a rock

DETERMINING AGE
OF ROCKS AND FOSSILS

FRANK K. MCKINNEY

THE Age of fossils intrigues almost anybody. Students not only want to know how former a fossil is, but they want to know how that historic period was determined. Some very straightforward principles are used to make up one's mind the age of fossils. Students should be able to empathize the principles and take that as a background so that age determinations by paleontologists and geologists don't seem similar black magic.

In that location are two types of age determinations. Geologists in the belatedly 18th and early 19th century studied stone layers and the fossils in them to decide relative age. William Smith was i of the most important scientists from this fourth dimension who helped to develop knowledge of the succession of unlike fossils by studying their distribution through the sequence of sedimentary rocks in southern England. Information technology wasn't until well into the 20th century that enough data had accumulated about the rate of radioactive disuse that the age of rocks and fossils in number of years could be determined through radiometric age dating.

This action on determining historic period of rocks and fossils is intended for 8th or 9th grade students. It is estimated to require four hours of grade time, including approximately one hr total of occasional didactics and caption from the teacher and two hours of group (team) and individual activities past the students, plus 1 hour of discussion among students within the working groups.

Explore this link for additional information on the topics covered in this lesson:

• Geologic Time

PURPOSE AND OBJECTIVES

This activity volition help students to have a amend understanding of the basic principles used to determine the age of rocks and fossils. This activeness consists of several parts. Objectives of this activeness are:
1) To take students determine relative age of a geologically complex area.
2) To familiarize students with the concept of half-life in radioactive decay.
3) To have students meet that individual runs of statistical processes are less predictable than the average of many runs (or that runs with relatively small numbers involved are less dependable than runs with many numbers).
4) To demonstrate how the rate of radioactivity and the buildup of the resulting disuse production is used in radiometric dating of rocks.
five) To use radiometric dating and the principles of determining relative age to evidence how ages of rocks and fossils tin can be narrowed even if they cannot exist dated radiometrically.
Return to top

MATERIALS REQUIRED FOR EACH GROUP

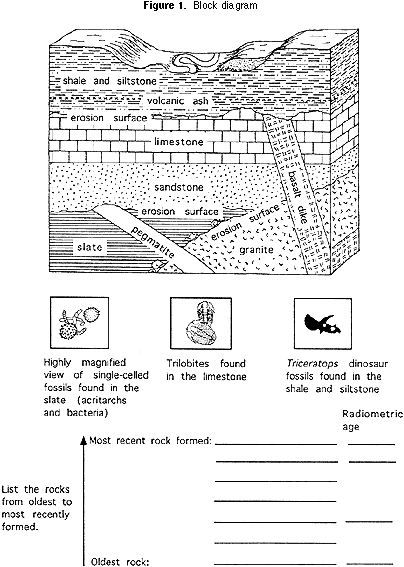
1) Block diagram (Figure one).
ii) Large cup or other container in which M & Thou'south can be shaken.
3) 100 G & M'southward
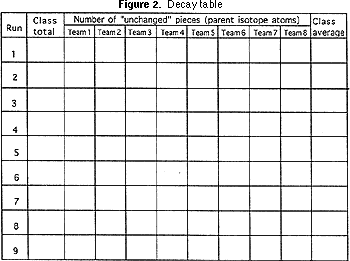
4) Graph paper (Figure two).
5) Watch or clock that keeps time to seconds. (A single spotter or clock for the unabridged grade will do.)
half dozen) Slice of paper marked Time and indicating either ii, iv, vi, 8, or x minutes.
7) 128 pocket-size cards or buttons that may be cut from cardboard or construction paper, preferably with a unlike color on opposite sides, each marked with "U-235" all on one colored side and "Pb-207" on the opposite side that has some contrasting color.

 

Render to top

PART 1: DETERMINING RELATIVE AGE OF ROCKS

Each team of 3 to 5 students should hash out together how to determine the relative age of each of the rock units in the block diagram (Figure one). After students have decided how to constitute the relative age of each stone unit, they should list them under the block, from most recent at the summit of the list to oldest at the lesser.

The teacher should tell the students that there are 2 bones principles used by geologists to determine the sequence of ages of rocks. They are:
Principle of superposition: Younger sedimentary rocks are deposited on meridian of older sedimentary rocks.
Principle of cantankerous-cut relations: Any geologic feature is younger than annihilation else that it cuts across.

PART 2: RADIOMETRIC AGE-DATING

Some elements have forms (called isotopes) with unstable atomic nuclei that have a trend to change, or decay. For example, U-235 is an unstable isotope of uranium that has 92 protons and 143 neutrons in the nucl eus of each atom. Through a serial of changes within the nucleus, it emits several particles, catastrophe up with 82 protons and 125 neutrons. This is a stable condition, and at that place are no more changes in the atomic nucleus. A nucleus with that number of protons is chosen lead (chemical symbol Pb). The protons (82) and neutrons (125) full 207. This particular form (isotope) of atomic number 82 is called Pb-207. U-235 is the parent isotope of Pb-207, which is the daughter isotope.

Many rocks contain modest amounts of unstable isotopes and the daughter isotopes into which they decay. Where the amounts of parent and daughter isotopes can be accurately measured, the ratio tin can be used to determine how old the stone is, as shown in the following activities.

Part 2a Activity — At any moment at that place is a small chance that each of the nuclei of U-235 volition of a sudden decay. That run a risk of decay is very modest, only it is e'er present and it never changes. In other words, the nuclei practice non "wear out" or get "tired". If the nucleus has non still decayed, at that place is e'er that same, slight chance that it will change in the almost future.

Atomic nuclei are held together by an attraction between the big nuclear particles (protons and neutrons) that is known as the "strong nuclear forcefulness", which must exceed the electrostatic repulsion between the protons within the nucleus. In general, with the exception of the unmarried proton that constitutes the nucleus of the most arable isotope of hydrogen, the number of neutrons must at to the lowest degree equal the number of protons in an atomic nucleus, because electrostatic repulsion prohibits denser packing of protons. But if there are too many neutrons, the nucleus is potentially unstable and decay may be triggered. This happens at any fourth dimension when improver of the fleeting "weak nuclear force" to the ever-nowadays electrostatic repulsion exceeds the binding energy required to concur the nucleus together.

Very careful measurements in laboratories, made on VERY LARGE numbers of U-235 atoms, have shown that each of the atoms has a 50:50 chance of decomposable during nearly 704,000,000 years. In other words, during 704 million years, half the U-235 atoms that existed at the offset of that time will disuse to Pb-207. This is known as the half life of U- 235. Many elements accept some isotopes that are unstable, substantially considering they have too many neutrons to be balanced by the number of protons in the nucleus. Each of these unstable isotopes has its own characteristic one-half life. Some half lives are several billion years long, and others are as short equally a x-thousandth of a second.
Return to top

A tasty way for students to sympathise about half life is to requite each team 100 pieces of "regular" One thousand & M processed. On a piece of notebook paper, each piece should be placed with the printed M facing downwardly. This represents the parent isotope. The candy should exist poured into a container large enough for them to bounce around freely, it should be shaken thoroughly, then poured back onto the newspaper so that it is spread out instead of making a pile. This starting time time of shaking represents one half life, and all those pieces of candy that have the printed M facing up represent a change to the daughter isotope. The team should pick up and gear up aside ONLY those pieces of candy that have the M facing upwards. Then, count the number of pieces of candy left with the Thou facing downwards. These are the parent isotope that did not change during the outset half life.

The teacher should have each team written report how many pieces of parent isotope remain, and the first row of the decay table (Figure 2) should exist filled in and the average number calculated. The same procedure of shaking, counting the "survivors", and filling in the side by side row on the decay tabular array should be washed seven or eight more times. Each fourth dimension represents a half life.

Afterward the results of the last "half life" of the M& G are nerveless, the candies are no longer needed.

Each squad should plot on a graph (Effigy 3) the number of pieces of candy remaining after each of their "shakes" and connect each successive point on the graph with a light line. On the aforementioned graph each team should plot the Average VALUES for the form as a whole and connect that by a heavier line. AND, on the same graph, each group should plot points where, after each "shake" the starting number is divided by exactly two and connect these points by a differently colored line. (This line begins at 100; the adjacent point is 100/ 2, or fifty; the next indicate is fifty/2, or 25; and so on.)

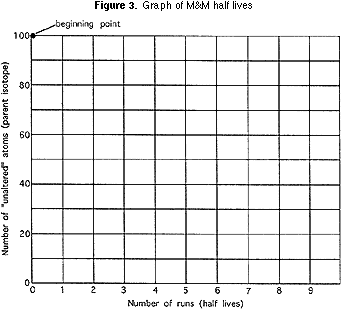Later on the graphs are plotted, the teacher should guide the course into thinking about:
1) Why didn't each grouping get the same results?
2) Which follows the mathematically calculated line better? Is it the single group's results, or is it the line based on the form average? Why?
3) Did students have an easier time guessing (predicting) the results when there were a lot of pieces of candy in the loving cup, or when there were very few? Why?

U-235 is found in about igneous rocks. Unless the rock is heated to a very high temperature, both the U-235 and its daughter Lead-207 remain in the rock. A geologist can compare the proportion of U-235 atoms to Pb-207 produced from information technology and determine the age of the stone. The next office of this practise shows how this is done.
Return to pinnacle

Function 2b Activity — Each team receives 128 flat pieces, with U-235 written on one side and Pb-207 written on the other side. Each team is given a piece of paper marked Time, on which is written either 2, iv, 6, 8, or 10 minutes.

The team should identify each marked piece then that "U-235" is showing. This represents Uranium-235, which emits a series of particles from the nucleus as it decays to Lead-207 (Pb- 207). When each team is ready with the 128 pieces all showing "U-235", a timed 2-infinitesimal interval should start. During that time each team turns over one-half of the U-235 pieces so that they now show Pb-207. This represents 1 "half-life" of U-235, which is the time for half the nuclei to change from the parent U-235 to the daughter Pb-207.

A new two-infinitesimal interval begins. During this time the team should turn over HALF OF THE U-235 THAT WAS LEFT Afterwards THE Outset INTERVAL OF Time. Keep through a full of iv to 5 timed intervals.

However, each team should Finish turning over pieces at the time marked on their TIME papers. That is, each team should stop co-ordinate to their Fourth dimension paper at the finish of the first timed interval (2 minutes), or at the end of the second timed interval (four minutes), so on. After all the timed intervals have occurred, teams should exchange places with one another as instructed by the teacher. The job now for each squad is to determine how many timed intervals (that is, how many half-lives) the set of pieces they are looking at has experienced.

The one-half life of U-235 is 704 meg years. Both the team that turned over a prepare of pieces and the second team that examined the set should determine how many meg years are represented by the proportion of U-235 and Lead-207 present, compare notes, and haggle about whatever differences that they got. (Right, each team must make up one's mind the number of millions of years represented by the set that they themselves turned over, PLUS the number of millions of years represented by the fix that another team turned over.)

Function 3: PUTTING DATES ON ROCKS AND FOSSILS

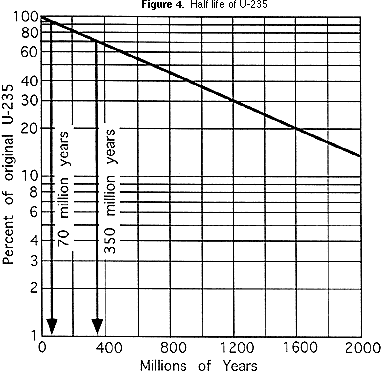
For the cake diagram (Effigy ane) at the start of this exercise, the ratio of U-235:Pb-207 atoms in the pegmatite is i:1, and their ratio in the granite is ane:3. Using the same reasoning about proportions as in Part 2b above, students can decide how erstwhile the pegmatite and the granite are. They should write the ages of the pegmatite and granite abreast the names of the rocks in the list below the block diagram (Figure one).

By plotting the one-half life on a type of scale known as a logarithmic calibration, the curved line like that for the Grand & MTM activeness can be straightened out, as y'all can see in the graph in Figure 4. This makes the bend more useful, because it is easier to plot information technology more accurately. That is especially helpful for ratios of parent isotope to girl isotope that correspond less than 1 half life. For the cake diagram (Effigy ane), if a geochemical laboratory determines that the volcanic ash that is in the siltstone has a ratio of U-235:Pb-207 of 47:3 (94% of the original U-235 remains), this ways that the ash is 70 million years one-time (see Figure 4). If the ratio in the basalt is seven:3 (seventy% of the original U-235 remains), then the basalt is 350 one thousand thousand years quondam (again, meet Figure 4). Students should write the age of the volcanic ash beside the shale, siltstone and basalt on the listing below the cake diagram.
Return to top

QUESTIONS FOR DISCUSSION

one) Based on the bachelor radiometric ages, tin can you determine the possible age of the rock unit that has acritarchs and bacteria? What is it? Why can't you say exactly what the age of the rock is?
ii) Can yous determine the possible historic period of the rock unit that has trilobites? What is it? Why tin can't you say exactly what the age of the rock is?
3) What is the age of the rock that contains the Triceratops fossils? Why tin can y'all be more precise about the age of this stone than you could most the ages of the stone that has the trilobites and the rock that contains acritarchs and bacteria?

Annotation for teachers: Based on cross-cut relationships, it was established that the pegmatite is younger than the slate and that the slate is younger than the granite. Therefore, the slate that contains the acritarch and bacteria is betwixt 704 one thousand thousand years and 1408 1000000 years old, because the pegmatite is 704 million years onetime and the granite is 1408 million years sometime. The slate itself cannot exist radiometrically dated, and so can only be bracketed betwixt the ages of the granite and the pegmatite.

The trilobite-bearing limestone overlies the quartz sandstone, which cross-cuts the pegmatite, and the basalt cuts through the limestone. Therefore the trilobites and the rock that contains them must exist younger than 704 million years (the age of the pegmatite) and older than 350 million years (the age of the basalt). The limestone itself cannot be radiometrically dated, and then can only be bracketed betwixt the ages of the granite and the pegmatite.

The Triceratops dinosaur fossils are approximately 70 million years old, because they are constitute in shale and siltstone that incorporate volcanic ash radiometrically dated at 70 one thousand thousand years. Any Triceratops institute beneath the volcanic ash may exist a little older than seventy million years, and any found above may be a piffling younger than 70 million years. The age of the Triceratops tin exist determined more closely than that of the acritarchs and bacteria and that of the trilobites considering the rock unit of measurement that contains the Triceratops tin can itself be radiometrically dated, whereas that of the other fossils could not.

---

samuelhencerel.blogspot.com

Source: https://ucmp.berkeley.edu/fosrec/McKinney.html

Share this post